In diesem Blogbeitrag wollen wir uns mit den theoretischen Grundlagen von Klassifikations-, Regressions- und Zeitreihenmodellen im Bereich des maschinellen Lernens beschäftigen, damit eine sinnvolle Auswahl zur Erstellung unseres Predicitive Planning-Modells erfolgen kann. Das entsprechende Modell wird im Vorhersage-Szenario in der Umgebung der SAP Analytics Cloud beschrieben und die dortigen Konfigurationsmöglichkeiten exemplarisch vorgestellt.
Hier geht es zu Predictive Planning | Teil 1: Predictive Analytics - ein Szenario vorbereiten!
Prognose-Szenario „Klassifikation"
Der Prognose-Szenario-Typ „Klassifikation" dient der Klassifizierung eines Datensatzes, der aus einer beliebigen Anzahl von Datensätzen besteht; es wird auf der Ebene des einzelnen Datensatzes kategorisiert (klassifiziert). Für die Klassifizierung stehen pro Datensatz nicht mehr als zwei verschiedene Kategoriewerte zur Verfügung.
Sie wollen zum Beispiel herausfinden, wer aus der Belegschaft einen Firmenwagen benötigt? Um diese Frage möglichst aussagekräftig zu beantworten, werden aus dem zugrunde liegenden Datensatz Entscheidungsregeln abgeleitet, die die Belegschaft möglichst genau in eine Gruppe A (Firmenwagen) und eine Gruppe B (kein Firmenwagen) einteilen.
Für Klassifikationsmodelle benötigen Sie einen Eingabedatensatz mit mindestens einer binären und mindestens einer zusätzlichen Variablen. Eine binäre Zielvariable enthält maximal zwei Gruppierungsklassen. Die Einflussfaktoren können entweder nominal (binär), ordinal oder kontinuierlich skaliert sein. Im Hinblick auf die eingangs gestellte betriebswirtschaftliche Frage nach den Dienstwagenberechtigungen ist in der Tabelle ein beispielhaftes Eingabedatenset dargestellt.
Die Aufgabe des Klassifikationsmodells ist es nun, mit Hilfe des Algorithmus aus der SAP Analytics Cloud anwendbare Entscheidungsregeln abzuleiten, um die Faktoren zu identifizieren, die zu einer genauen Gruppierung führen. Die SAP Analytics Cloud verfolgt dabei einen Self-Service-Ansatz, der für den Laien sinnvoll ist, aber bei Experten zu Verwirrung führen kann, da die Art und Weise, wie die Bewertungsalgorithmen verfahren, nicht offengelegt wird. Sie liefern somit nicht die gewünschte Transparenz über das verwendete Verfahren. Klassische und aktuell populäre Verfahren für die Klassifikation sind beispielsweise:
- Logistische Regression
- Nearest Neighbour
- Decisiontrees
- Random Forest
- Bagging
- Gradient Boosting
- XGBoost
- Support Vector Machines
Diese sind jedoch (noch) nicht in der Form auf der SAC wählbar.
Für unser spezifisches Beispiel ist das Verfahren ohnehin nicht zielführend. Dementsprechend müssen wir uns nun das nächste Prognose-Szenario genauer anschauen - die Regression.
Prognose-Szenario „Regression"
Die Regression ist eine der bekanntesten statistischen Analysemethoden zur Ableitung und Überprüfung von Korrelationsmustern. Regressionen sind insbesondere für ihre Fähigkeit zur schnellen Gewinnung von Einsichten in große und manchmal unverständliche Datensätze populär. Sie können zum Beispiel verwendet werden, um mit Verkaufszahlen und Marketingausgaben den besten Vertriebskanal zu ermitteln.
Die Regressionsanalyse ist ein Werkzeug zur Untersuchung von direktionalen Beziehungen zwischen Variablen. Eine gerichtete Beziehung bedeutet, dass eine Variable eine andere Variable beeinflusst oder vorhersagt. Variablen, die eine andere Variable beeinflussen, werden Prädiktoren oder in der SAP Analytics Cloud als Einflussfaktoren bezeichnet. Diese Einflussfaktoren beeinflussen ein Kriterium - in der SAP Analytics Cloud ist dies eine Zielvariable.
Gerichteter Zusammenhang
Prädikator -> Kriterium
Einflussfaktor -> Zielvariable
Wenn ein Einflussfaktor eine Zielvariable vorhersagt, spricht man von einer einfachen Regression. Sobald es mehrere Faktoren gibt, spricht man von einer multiplen Regression. Sowohl bei der einfachen als auch bei der multiplen Regression kann nur eine metrisch skalierte Zielvariable vorhergesagt werden. Da die meisten Kriterien nicht durch einen einzigen Einflussfaktor erklärt werden können, wird in der Praxis für gewöhnlich die multiple Regression eingesetzt.
Multiple Regression
Einflussfaktor 1 ->
Einflussfaktor 2 -> Zielvariable
Einflussfaktor n ->
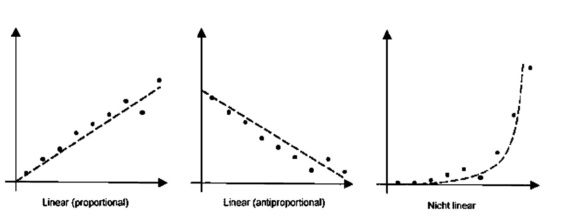
Der Zusammenhang zwischen Einflussfaktor(en) und Zielvariable kann linear oder nicht-linear sein.
Bei einer linearen Beziehung stehen der / die Einflussfaktor(en) und die Zielvariable in einer konstanten Beziehung zueinander, die entweder proportional oder antiproportional sein kann. Nichtlineare Zusammenhänge zeigen kein konstantes Verhältnis, sondern zum Beispiel ein exponentielles Wachstum oder eine U-Kurve. Je nach Art der Beziehung wird eine andere Regressionsmethode nötig. Dementsprechend müsste die Art der Korrelation normalerweise anhand von Streudiagrammen grafisch überprüft werden, um eine geeignete Regressionsmethode auswählen zu können.
Die SAP Analytics Cloud wählt automatisch die richtige Regressionsmethode auf Basis der Parametrisierung des Regressionsmodells. Diese Blackbox ist für Laien, ähnlich wie bei der Klassifizierung sicherlich nützlich, für Experten führt sie jedoch zu einer Intransparenz des Regressionsmodells. Es ist daher empfehlenswert, den Korrelationstyp vorab zu überprüfen. Dafür muss lediglich eine Story mit der Darstellung der Korrelation in einem Punktediagramm erstellt werden. Ein Klassifikationsmodell lässt sich in ein Regressionsmodell überführen, indem die Wahrscheinlichkeit der Zugehörigkeit zu einer Klasse bestimmt wird.
Beweisen Regressionen kausale Zusammenhänge?
Ein Ziel wissenschaftlicher Untersuchungen ist die Identifizierung von Ursachen und Muster zu erkennen, um gezielte Maßnahmen zur Beeinflussung dieser Muster anwenden zu können. Grundvoraussetzung für Kausalität ist die Identifikation von Zusammenhängen, im ersten Schritt ohne Wirkungsrichtung. Mit Hilfe von zwei Beobachtungen zu unterschiedlichen Zeitpunkten, z. B. vor dem Training und nach dem Training, kann sichergestellt werden, dass eine bestimmte Ursache zu einer Wirkung geführt hat. Durch die zeitliche Fixierung von Ursache und Wirkung werden die Einflussfaktoren und die Zielvariable bestimmt; in Regressions- und Klassifikationsmodellen wird der gerichtete Zusammenhang bestimmt.
Um diese Aussage zu bestätigen, müssen alternative Erklärungen ausgeschlossen werden. Ein klassisches Beispiel für eine falsche Interpretation von Kausalitätsinterpretation ist die einfache Korrelation zwischen dem Rückgang der Kindergeburten und der Anzahl der Störche in Deutschland. Nur weil zwei stark korrelieren, bedeutet das nicht unbedingt, dass eine Kausalität vorliegt. Mit Hilfe von experimentellen Methoden kann man gezielt die Ursache beeinflussen und die Wirkung bestimmen, um einen kausalen Zusammenhang zu belegen.
Nachweis eines Kausalzusammenhangs
Die Messung der Wirkung kann z. B. durch den Vergleich einer Gruppe mit Einfluss und einer Gruppe ohne Einfluss belegt werden.
Da in der SAC keine automatische Kausalitätsprüfung durchgeführt wird, ist es ungemein relevant, die Anwendung der Ergebnisse zu verifizieren.
Für unser spezifisches Beispiel ist auch dieses Verfahren nicht zielführend. Sehen wir uns also das Prognose-Szenario der Zeitreihe an.
Prognose-Szenario „Zeitreihe"
Die Zeitreihe, eine Spezialform der Regression, ist eine mathematisch-statistische Analyse historischer Datenpunkte. Der wesentliche Unterschied zur Regression ist, dass keine Korrelationsmuster zwischen Variablen ermittelt werden (Querschnittsanalyse), sondern eine Prognose von Erwartungswerten für zukünftige Daten auf der Basis historischer Datenpunkte (Längsschnittanalyse) getroffen wird. Ein einzelner Datenpunkt einer Zeitreihe besteht immer aus einer Zeit und einem Wert, z. B. ist die Aufzeichnung der Anzahl der Regenstunden pro Tag in Bielefeld ein Datenpunkt.
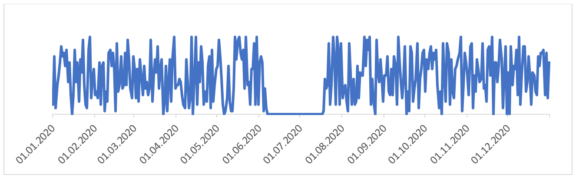
Das primäre Ziel der Zeitreihenanalyse, und damit auch des Prognoseszenarios Zeitreihe, ist die ausschließliche Vorhersage der Werte zukünftiger Datenpunkte. Aus diesem Grund muss der Eingabedatensatz für eine Zeitreihenprognose mindestens das Datenpaar Datum und Wert enthalten. Datenpaare werden bei Zeitreihen als Signal bezeichnet und die historischen sowie zu prognostizierenden Werte durch eine Zielvariable beschrieben, z. B. die Regenstunden pro Tag (in Bielefeld). Wenn wir die Zeitreihe vom Eingabedatenset in ein Liniendiagramm transformieren und die Signale miteinander verbinden, erhalten wir den in der Abbildung sichtbaren Verlauf.
Die x-Achse zeigt das Datum (Tag) und die y-Achse die Regenstunden pro Tag. Eine Frage daraus könnte beispielsweise sein: „Mit welchen Regenstunden pro Tag müssen wir im ersten Quartal 2021 rechnen?“
Um die Prognosewerte zu ermitteln, benötigen wir einen Eingangsdatensatz mit historischen Signalen, um überhaupt Prognosewerte ermitteln zu können. Für die Ermittlung zukünftiger Prognosewerte sind die historischen Signale unverzichtbar; sie bilden die Grundlage für die Bestimmung eines Algorithmus, der für die Ermittlung zukünftiger Prognosewerte verwendet werden kann. Für einen zufriedenstellenden Algorithmus ist ein Minimum an historischen Signalen erforderlich. In der SAP Analytics Cloud ist die Voraussetzung ein Verhältnis von 5:1, um überhaupt einen Prognosewert mit einem Konfidenzintervall berechnen zu können.
Dies führt zu einer grundlegenden Frage, die Sie sich stellen sollten, bevor Sie Zeitreihen verwenden: „Welcher Prognosehorizont soll festgelegt werden und sind dafür genügend historische Signale im Eingangsdatensatz vorhanden?" Existieren nicht genügend historische Signale im zu verarbeitenden Eingabedatenset, werden in der SAP Analytics Cloud eine Warnmeldung oder eine Abbruchmeldung ausgegeben.
Im Zusammenhang mit der Anwendbarkeit von Zeitreihen betrachten wir das Verhältnis 5:1, aber ebenso wichtig ist der Aspekt der Granularität der Daten. Wenn Ihre historischen Daten jeden Monat, jede Woche, jeden Tag, jede Stunde, jede Minute oder sogar jede Sekunde aufgezeichnet werden, dann werden die Prognosen in derselben Zeiteinheit erstellt. Das heißt, wenn Sie Jahreswerte haben, können Sie keine Prognosen auf Tagesebene erstellen!
Dies ist jedoch durch eine vorherige Aggregation des Eingabedatensatzes möglich. Das heißt, wenn die Daten jede Minute von Sensoren aufgezeichnet werden (aber die Minute für Ihren Anwendungsfall nicht relevant ist), benötigen Sie eine höhere Zeiteinheit wie Stunde oder Tag. In diesem Kontext verwenden Sie eine Aggregationsfunktion für die Transformation, z. B. wird ein Stundenwert aus 60 gemessenen Einzelwerten in Minuten zusammengesetzt. Dies kann der erste, der letzte, der Durchschnitt oder ein berechneter Wert sein (z. B. Durchschnitt oder eine komplexere Formel). Ein wichtiger Punkt ist die Größe der Aggregation. Eine große Aggregation kann Informationen verbergen, die unentdeckt bleiben sollten, was zu einer Verschlechterung der Qualität der Vorhersage führen würde.
Als letzte Vorarbeit sollte noch das Eingabedatenset mit den historischen Signalen chronologisch sortiert und verifiziert werden, dass jeder Datenpunkt nur einem Wert der Zielvariablen entspricht. Wenn alle Grundvoraussetzungen erfüllt sind, wird auf Basis der historischen Signale in der SAP Analytics Cloud ein maschinelles Lernen durchlaufen, das den besten Algorithmus zur Berechnung der Prognose für die Zielvariable und dem entsprechenden zukünftigen Horizont anwendet.
Für unser spezifisches Beispiel ist das Verfahren offensichtlich passend. Dementsprechend werden wir im nächsten Blog mit dem Beispiel nun eine Zeitreihenanalyse durchführen.